

Reference:įrom the source of Wikipedia: Inverse Laplace transform, Mellin’s inverse formula, Post’s inversion formula.įrom the source of Paul’s online notes: Inverse Laplace Transform, Factor in the denominator, Term in partial fraction decomposition.įrom the source of Science Direct: Linear Systems Analysis, inverse transform, Additive property, First shift theorem, The Convolution Theorem.Both Laplace transform and Fourier transform are integral transforms, which are most commonly employed as mathematical methods to solve mathematically modelled physical systems. The inverse Laplace with steps transform can more easily solve the problems in technical applications in real life and makes the differential equations simple to solve. Use this online inverse Laplace transform calculator with solutions, which solves differential equations by transforming one form F(s) into another simple form f(t). Rest you can also use the best inverse fourier transform calculator to speed up your calculations. This is achieved by using the inverse fast Fourier transform IFFT. The Fourier transform is used to transform the signal from the time domain to the frequency domain, and the inverse Fourier transform is used to transform the signal from the frequency domain back to the time domain. What does inverse Fourier transform can do?
The Laplace transform is a constant multiplied by a function with an inverse constant. The sum of the two separate terms is the reciprocal of the sum of the inverse transformation of each term that you could also go to determine by this online inverse transformation calculator, the latter being considered separately. What is the inverse of Laplace’s constant? The Laplace transform provides some useful techniques to determine certain types of differential equations when the initial conditions are met, especially when the original value is zero. You can transform many equations with this Laplace step function calculator numerous times quickly without any cost.įAQ: What is the importance of the inverse Laplace transform online?.The Laplace inverse calculator with steps transforms the given equation into a simple form.Hit the calculate button to see the results.Enter a complex function F(s) and see the equation preview in Laplace form.How Inverse Laplace Transform Calculator Works?Īn online inverse Laplace calculator with solution allows you to transform a complex Function F(s) into a simple real function f(t) by following these instructions: Input: However, an online Riemann Sum Calculator helps you to approximate the definite integral and sample points of midpoints, right and left endpoints using finite sum. If given the two Laplace transforms G (s) and F (s), then It can be proved that if the function F(s) has the inverse Laplace transform with steps as f(t), then f(t) is uniquely determined (considering that the function is divided only by a set of distinguishing points, use the same Null Lebesgue metric). The inverse Laplace transform with solution of the function F(s) is a real function f(t), which is piecewise continuous and exponentially restricted. However, an Online Laplace Transform Calculator provides the transformation of the real variable function to the complex variable. Let us start over from the perspective of the real variable t and obtain the function of f(t).
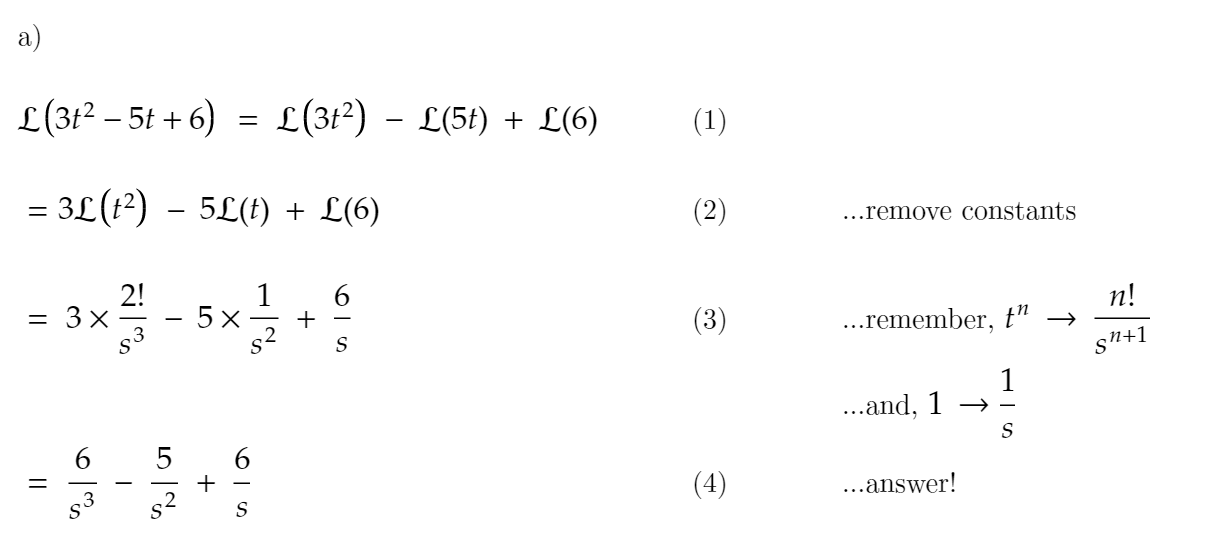
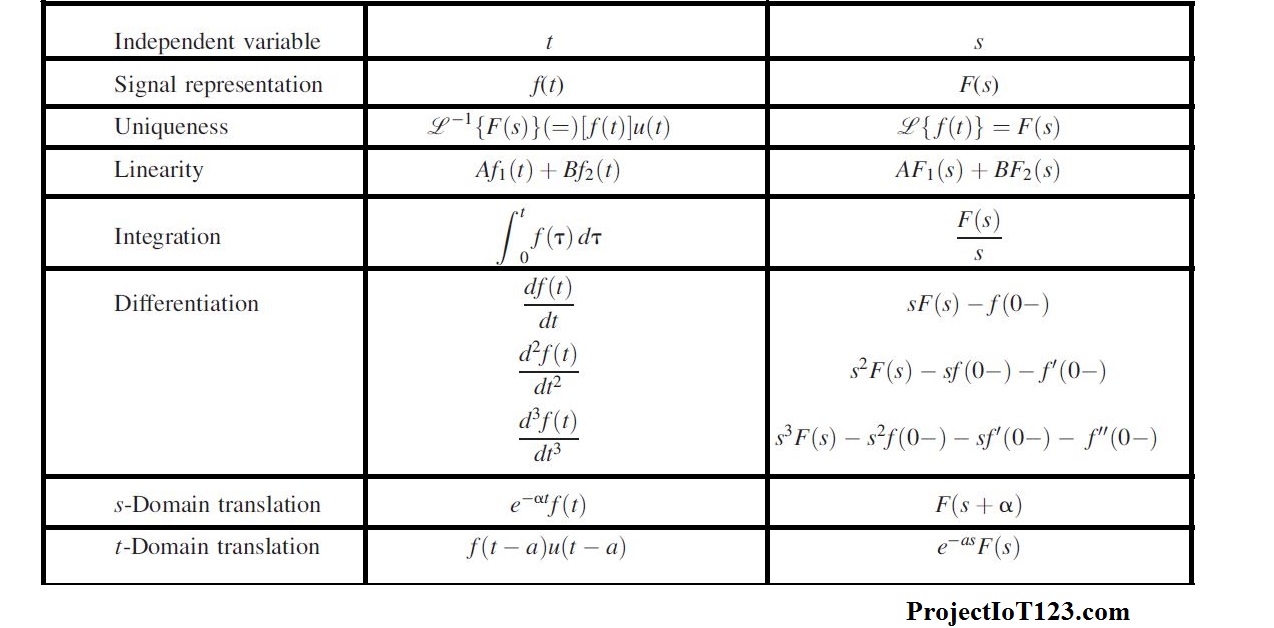
If the Laplace inverse formula corresponding to each part of F(s) found on the table, then the inverse Laplace Transform calculator can be transformed. Ideally, we want to simplify the F(s) of the complex variable to the point where we make the comparison for the formula from an inverse Laplace transform table. In mathematics, the inverse Laplace transform online is the opposite method, starting from F(s) of the complex variable s, and then returning it to the real variable function f(t).
#Laplace transform chart how to
So, start learning to understand how to the inverse Laplace transform of the functions step by step with the help of an example and inverse Laplace table. The inverse Laplace calculator has several properties that make it useful for analyzing linear dynamical systems. An online inverse Laplace transform calculator will convert the complex function F(s) into a simple function f(t) in the real-time domain.


 0 kommentar(er)
0 kommentar(er)
